NCR Program - 01/01/19

The mathematical function 'nCr' is used when calculating how many different times a fixed number of items (determined by r) can come up in a list n items long. For example, if there are six people lined up in a fixed row, how many ways can two people occur in this line? The first and last people may be chosen, the second and last people may be chosen, etc. The nCr function calculates the total number of possible fixed ways in which r may come up in n terms. Since it is tedious to manually work out the number of ways in which a fixed number may come up, especially as the length of the list increases, it is desirable to use the nCr function as an alternative.

Using factorials (denoted by a '!'), it is possible to write what the nCr function does in the following form:

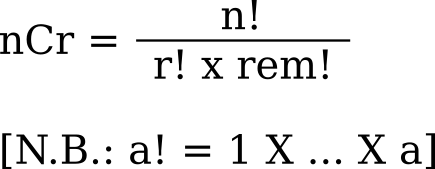
In the above image, 'r' corresponds to the number of items to come up, 'rem' corresponds to the number of items which would remain in the list after 'n' items had been removed, and 'n' corresponds to the total number of items in the list.

Below, you can see a Python3 program which implements this function. It first asks the user for the total number of items in the list and then asks for how many items are to be selected (the 'success' value). After having gathered this data, it carries out the necessary factorial operations and then outputs the nCr result using the method from above. The code is run using an embedded Trinket interpreter: